行列式的秩 行列式的秩和行列式的值有什么关系
在工程和科学领域,线性代数的概念如矩阵和行列式常被广泛应用,尤其在处理几何问题时显得尤为重要。本文将深入探讨面积及其在高维空间中的推广,揭示其背后的数学原理与实际应用。
1: 面积的基本概念
当提到面积,许多人首先想到的就是长乘以宽,但这仅是二维情况下的简化定义。实际中,我们讨论的面积是源自平行四边形的几何特性。根据几何学,平行四边形的面积定义为相邻两边的长度乘以它们夹角的正弦值。这一基本概念为我们理解更复杂的高维面积奠定了基础。
随着对高维空间问题的探索,面积的定义也需要扩展。需要注意的是,面积作为一个标量,源自相邻两个边的矢量相乘。我们可以将面积视作一种映射关系,关联了两个矢量的表现。
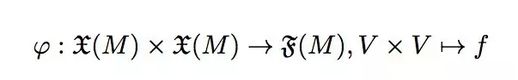
在这个映射中,V代表一个适量,而V*V则形成两个适量的有序对。由此,自然可以推导出所求的面积。
为了证明这个映射是线性的,首先考虑一个简单的例子。假设我们有两个单位向量(1,0)和(0,1),它们分别在X轴和Y轴上构成一个正方形。根据面积的定义,这个正方形的面积为1(1*1=1)。

接下来,若将第一个矢量缩放为a倍,面积也随之变为a倍;若第二个矢量缩放为b倍,面积则变为b倍。当同时对两个矢量进行ab倍的缩放,面积则变为原来的ab倍。这表明,面积映射对矢量标量积是线性的,如下所示:
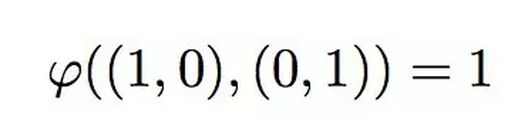
进一步分析,面积的映射对于矢量加法同样是线性的。由于矢量加法本身的线性特性,其对应的面积映射也遵循这一规则。通过几个示例,我们可以探讨映射加法线性的影响。
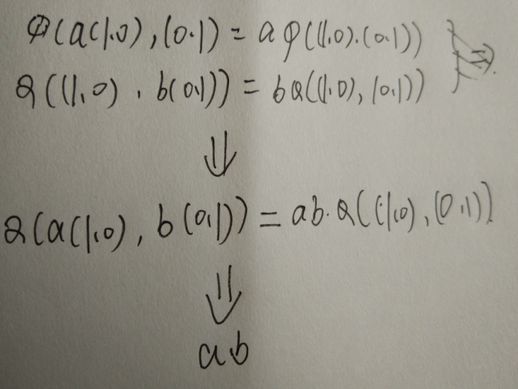
考虑两个共线矢量所形成的平行四边形,其面积为零。假设面积映射是关于适量加法的线性映射,则我们可得如下结果:
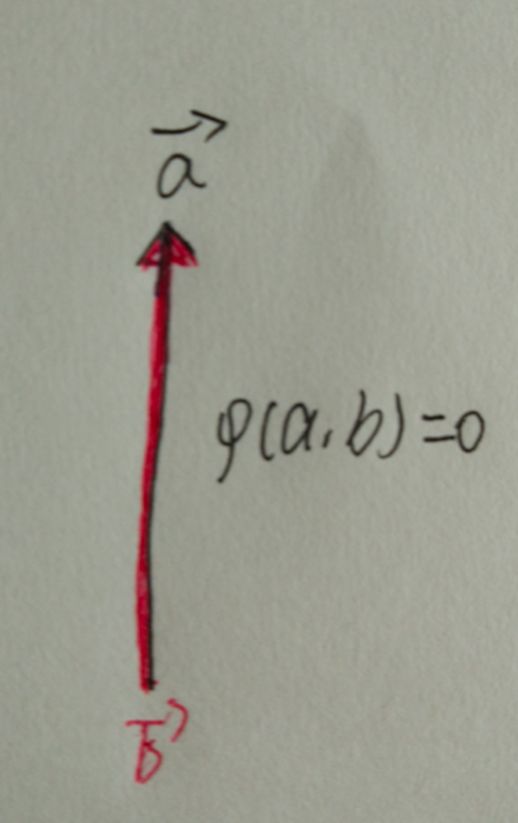
这一推理中引入了一个重要理论:在交换相互垂直的操作数的顺序后,面积映射可能变为负值。这一符号的选择取决于定义,一般我们将X轴的矢量放在前,Y轴的矢量放在后,从而得到一个平行四边形的面积为正值。
2: 三维空间中的应用
在三维空间中,我们通常使用右手定则来进行实验。如果以X轴的方向为“头”,Y轴为“尾”,则纸面方向向外代表面积的正方向。反之,纸面向内则表示方向相反,正负号的几何意义在此变得更加明显。
我们可以利用任意两个矢量所形成的平行四边形来表示其面积,具体公式如下:
通过分析,我们可以看出,面积实际上就是一个2×2矩阵的行列式,具体如下:
我们的第一行是第一个向量(a, b),第二行是第二个向量(c, d)。无论是以行向量还是列向量的形式书写,结果都不影响行列式的值。
3: 行列式的计算性质
在上面的推导中,我们发现行列式的值与行向量或列向量的排列无关。这也解释了为何在计算行列式时,行列的地位是对等的。当我们交换向量顺序时,面积出现负号的现象正是这一原理的体现。行列式的其他计算性质也反映了面积映射的线性特征。
行列式实际上是面积概念的推广。在给定一组基的情况下,N个向量所张成的N维广义体积就是行列式的核心意义。
4: 行列式的进一步推广
根据上述结论,我们可以轻松推广至三维体积的计算。行列式的定义涉及每一行不同列元素的乘积,符号与逆序性相关。逆序性在几何上意味着在规定一个正方向后,交换任意一对数时均需取负号。这一特性同样适用于体积的计算,更高维度的广义体积也有类似的正方向概念,只是难以用直观的方式表示。
通过对不同行列元素乘积的分析,我们理解了反对称性的重要性。如果有任意两个元素在同行同列,交换列指标后的乘积不变,但符号相反,这就意味着乘积必须为零,因此在行列式的值中未体现。
行列式的定义看似复杂,但实质上源于面积映射的反对称性。二维的面积映射可以扩展到多维,从而形成R维的行列式表现。
5: 行列式与矩阵的逆
许多定理表明,行列式为零的矩阵不可逆,而非零的矩阵则可逆。这让我们思考,行列式作为面积的代表,是如何与线性变换的可逆性结合在一起的。
当我们将一组线性无关的矢量写为列向量时,它们所张成的N维体积不为零,具体值由行列式决定。在经过线性变换A后,新的向量形式如下:
A为N*N矩阵,向量为列向量。变换前的N维体积为:
变换后的N维体积是:
当A的行列式不为零,说明变换后N维体积依然存在。结合线性无关性与体积特性,我们得出结论:
如果A的行列式不为零,则A可以将一组线性无关的矢量映射为另一组线性无关的矢量;反之,若A的行列式为零,映射将产生线性相关的矢量。
如果A的行列式为负,体积的方向将发生改变。
6: 秩
尽管行列式A不能确保所有矢量线性无关,但它能够保证少数矢量的线性无关性,这个数量称为线性变换A的秩。例如,一个秩为2的3*3矩阵A,经过变化后,三维体积将退化为零,但仍能保持一个面积不为零的面。
线性变换的秩即为变化后仍能维持非零体积的最大维度。
理解了秩、行列式和可逆性的几何意义后,我们可以构造出一种线性变换A,使其要么保留所有几何体,要么降维为特定结构。这种现象可以视为“降维打击”。
对于更高维度的推理,感兴趣的读者可以自行探索。如有疑问,欢迎在评论区讨论,期待与大家的交流与探讨。

