约分怎么约 约分简分数怎么做
3九章算术卷第一方田——约分术
原文
在古代,数学的发展展现出人类智慧的结晶,其中的约分术便是一个典型的例子。这项技术不仅简单实用,还体现了古人对数字的深刻理解。现今,我们可以借助这些智慧,来探索约分的奥秘。
考虑分数十八分之十二,问其约分结果为多少?答案是三分之二。同样地,若分数为九十一分之四十九,经过约分,结果为十三分之七。
古人总结约分的方法是:如果分子和分母均为偶数,则可以将其各自减半;而若不是,则需要借助算筹将分子和分母重新排列,通过相减逐步寻找最大公约数,最终实现约分。
例如,对于九十一与四十九的约分过程,可以如下进行:
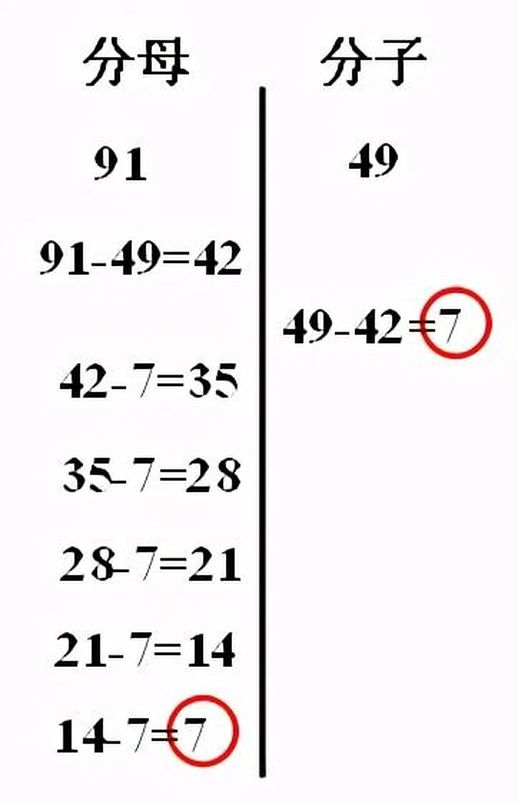
在此,我们需要找到91与49的最大公约数,而这一过程被称为更相减损术,或者辗转相减法。通过一系列的减法运算,最后我们确定91与49的最大公约数为7。

评议:
本节内容讲解了《九章算术》中关于约分的技巧。我们需要明确的是,约分的关键在于找到分子和分母的最大公约数。而如何找到这个最大公约数呢?古人通过发明更相减损术提供了一种有效的解决方案。深入学习这一方法后,笔者不禁感慨,古人的智慧与创造力确实令人敬佩。
1、“更相减损术”的历史与实用性
更相减损术作为古代求解最大公约数的一项重要创举,其简单性和实用性令人称道。在小学阶段,我们学习过短除法来寻找两数的最大公约数,而在大学阶段则接触过辗转相除法。通过研究《九章算术》,我们更能体会到这两者间的异同。虽然更相减损术的步骤相对繁琐,但减法运算比除法更加直观,且不必处理余数问题,最终可以快速获得结果。
更相减损术与欧几里得的辗转相减法思路相似,表明了在不同文明背景下,人类对数学问题的探索和思考展现了独特的创造性。
2、古人对数学简洁性的追求
刘徽在讨论约分时提到“繁则难用”,并通过例子说明,例如四分之二可表示为八分之四,但经过约分则简化为二分之一。由此可见,古人对于化繁为简的追求不仅体现了实用性,更展现了数学形式上的美感,这种思想与世界数学史上追求简洁的趋势是一致的。

3、分类与化归的智慧
在约分术的应用中,古人能够清楚地区分两种情况:一种是分子分母均为偶数,另一种则是它们不全为偶数。对这两种情况采用不同的处理方法,展现出古人对数学分类与化归思想的运用。这种逻辑思维能力,令现代人倍感惊叹。
4、循序渐进的教育理念
在解题时,题目[5]的分数可以通过“九九表”迅速找到最大公约数,而题目[6]则相对复杂,正好体现了古代数学教育的原则:由易到难,循序渐进。这一理念至今仍在我们的教育体系中得以延续,显示了古人与现代教育思想的深刻联系。

5、对“以少减多”的理解
在翻译“以少减多”时,笔者曾感到困惑,直到经过一番思考与讨论才逐渐理清了这一短语的含义。实际上,这是指用大数减去小数,形成了一种从多中减去少的标准,使得问题的解决方式更为清晰。
6、一点说明
关于更相减损术的数学证明,在此不作详细阐述,感兴趣的读者可以自行探索和验证。
参考文献
1、肖作政编译.《九章算术今解》.大连:辽宁人民出版社,1990
2、郭书春译注.《九章算术译注》.上海:上海古籍出版社,2009
3、钱宝琮点校.《算经十书》.北京:中华书局,2021
4、邹涌译解.《九章算术》.重庆:重庆出版社,2015

