矩阵的行列式怎么求 det矩阵A

在数学中，行列式是一个重要的概念，它为解决线性方程组和多种应用提供了基础。通过对矩阵的深入理解，我们能够更好地掌握行列式的计算和性质，进而应用于工程、经济和科学等多个领域。以下将对行列式的定义及计算方法进行详细解析。

一组数以行和列的形式排列即形成了矩阵。

例如，上述矩阵由两行三列组成。矩阵在现代线性代数中占据了核心地位，帮助我们以简洁的方式表示代数方程。

代数方程能够转化为矩阵形式，以下是一个三元一次方程组的例子：

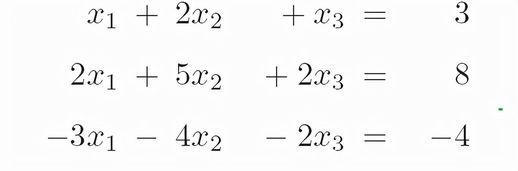
若将其表示为矩阵的形式，便可将系数整理到一起：

为确保相关解的唯一性，计算行列式的值至关重要。在工程、经济以及科学研究中，行列式的应用十分广泛。本节将重点讨论三阶及以下的行列式基本知识。

定义

: 对于任意n阶方阵A，其对应的行列式被称为A的n阶行列式。

1阶行列式 (1×1)

考虑一个矩阵a=[a]，那么该矩阵的行列式直接等于a。

二阶行列式 (2×2)

当矩阵的阶数为2时，行列式的定义为矩阵A的值：

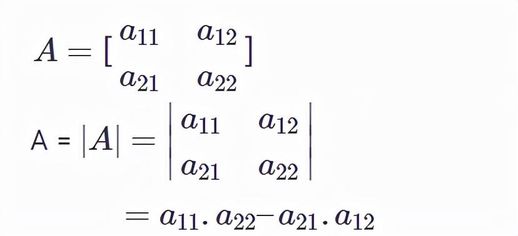
接下来，我们可以计算3×3阶的行列式。

三阶行列式 (3×3)

假设有一个3阶矩阵A：

那么，该矩阵的行列式计算方式为：

|A|=a11a22a33 + a12a23a31 + a13a21a32 – a11a23a32 – a12a21a33 – a13a31a22

注意：主对角线上的元素带有正号，而副对角线上的元素则带有负号。

行列式的特性

现在我们将探讨行列式的一些基本特性：

性质1

- 行列式在行和列互换时，其值保持不变。

性质2

- 如果任意两行（或两列）互换，则行列式的符号会改变。

性质3

- 当任意两行或两列相等时，行列式的值为零。

性质4

- 如果某行或某列的每个元素都乘以常数k，则行列式的值也会乘以k。

利用行列式求三角形面积

已知三角形的顶点为(x1，y1)、(x2，y2)和(x3，y3)，其面积可以通过公式计算：

A = 1/2[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]

此公式可改写为行列式的形式，从而更加简洁明了。

利用行列式解二元一次方程组

考虑已知的方程组，它可以被表达为AX = B，其中A是系数矩阵：

利用消元法可获得相应的结果：

我们将上述结果再通过行列式表达：

行列式不仅是线性代数中的一项基本工具，更是理解复杂数学模型的重要桥梁。通过对行列式的深入探索，我们能够更好地掌握其在实际问题中的应用，从而在各个领域中获得更大的成功。