矩阵的秩怎么理解 矩阵的秩是方阵吗
在探讨几何学的核心概念时,面积的定义和高维推广是非常重要的主题。通过对这些基本概念的深入分析,我们不仅能更好地理解线性代数的原理,还能掌握其在更高维度中的应用。接下来,我们将详细探讨面积的定义、相关的线性映射,以及行列式在几何中的作用。
1: 什么是面积?
提到面积,许多人首先联想到的便是长乘以宽。这里所讨论的面积实际上是欧几里得空间中的几何基础单位:平行四边形的面积。平行四边形的面积可以通过其相邻两边的长度与夹角的正弦来计算。
面对更复杂和高维的问题时,我们必须扩展这一基本定义。面积作为一个标量,来源于两个相邻边所构成的矢量的乘积,因此应当将面积视为一种映射关系。
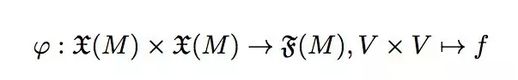
在此,V可视作一个矢量,V*V则代表两个有序矢量的组合,而f即为所求的面积。
为了证明这一映射的线性特征,我们可以从一个简单的例子出发。设定第一个矢量为(1, 0),第二个矢量为(0, 1),这两个单位矢量所构成的四边形实际上是一个正方形。根据面积的定义,面积计算为1乘以1,即为1。
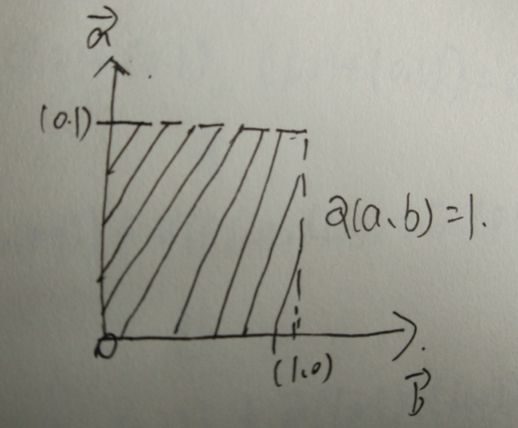
接着,如果将第一个矢量缩放为a倍,面积也将相应地变为a倍。如果将第二个矢量缩放为b倍,面积同样会变为b倍。若同时对两个矢量缩放为ab倍,面积也会相应地变为原来的ab倍。这说明,面积映射对于标量的线性变换是显而易见的,如下所示:
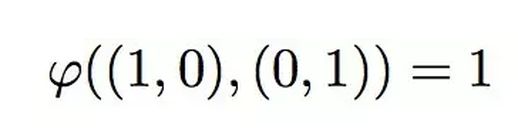
在实际应用中,面积的映射同样遵循矢量加法的线性特性。由于矢量加法本身就是线性的,因此其对应的面积映射也自然而然地是线性的。接下来,通过几个实例,来说明这一线性映射的一些结果。
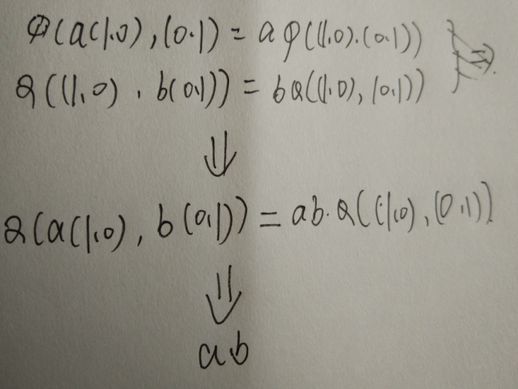
当两个共线矢量构成的平行四边形退化为一条直线时,面积便为0。假设面积映射是关于适量加法的线性映射,则可以得出以下结论:
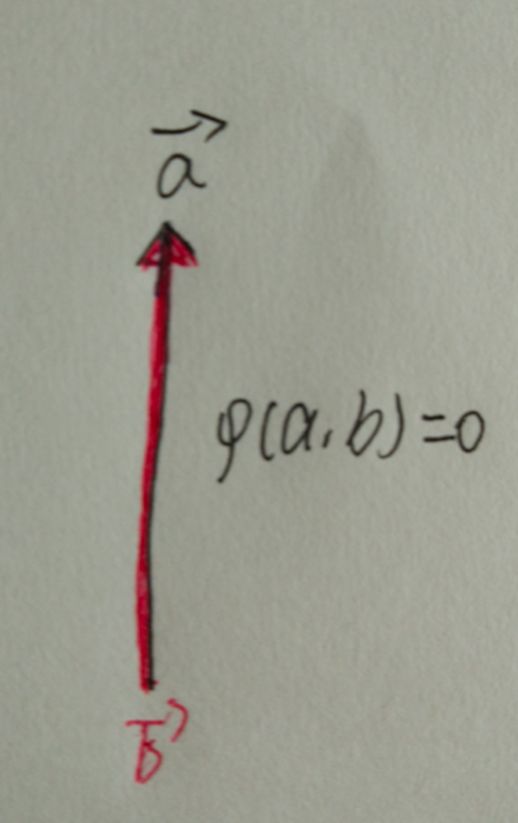
在这里,我们应用了一个理论:交换两个垂直矢量的顺序会使面积映射变为负值,这取决于我们所定义的方向。通常情况下,X轴的矢量在前,Y轴的在后,由此形成的平行四边形的面积被视为正值。
2: 三维空间里的应用
在三维空间中,我们通常通过右手定则来进行实验。若以X轴的正方向为手指,Y轴的正方向为手掌,右手定则则告诉我们,纸面向外的方向即为面积的正方向。反之,纸面向内则为负方向,这使得正负号的几何意义愈加明显。
我们可以用平面内任意两个矢量构成的平行四边形面积来表示,实际上,这可以通过一个2x2的矩阵的行列式来求得,如下图所示:
第一行对应第一个行向量(a, b),第二行则为第二个行向量(c, d)。如何将矢量表示为行向量或列向量取决于我们的需求。
3: 行列式的性质计算
通过以上推理,我们可以清晰地看到,行列式的值与行列的排列方式无关。这也是为何在计算行列式时,行列的角色是对等的。值得注意的是,根据前面的分析,交换向量顺序时,面积为负的原因,这就是在行列式中,交换行向量或列向量会导致符号变化的原因之一。
行列式实际上是面积概念的一个扩展。在给定一组基的情况下,N个向量构成的N维广义四边形的体积正是行列式的本质所在。
4: 行列式的推广
基于上述结论,我们可以很方便地将其推广至三维体积的计算。需要注意的是,行列式的定义实际上是通过选择每一行不同行的元素乘积,并且根据逆序性来调整符号。逆序性的几何意义在于规定了一个正方向,交换任意一对数值就会引入负号。这样的性质在面积函数中同样得到了体现,而高维体积的推广则正是受限于右手法则的局限性。
此处,交换任何一组指标的操作便会改变符号,这被称为反对称性。为什么选择不同行不同列的元素进行乘积,其原因在于,如果有任意两个元素是同行同列的,交换后乘积不变但符号相反,这使得乘积必须为0,这就是行列式值中不体现的原因之一。
实际上,行列式的定义相对复杂,但它的本质与广泛的面积映射反对称性息息相关,面积映射是一个二维的概念,而我们可以将其推广至多维空间,发现R维形式与R*R的行列式形式完全一致。
各维度所代表的意义也可以做一个二维代表平面面积,三维则是空间体积,四维为超体积,依此类推。在上述推理中,给定的基坐标所写出的矩阵必为方阵,而矩阵的行列式则对应于面积或体积。这样的推广在大多数线性代数教材中都会提及。
5: 行列式与矩阵的逆
我们知道许多定理,比如行列式为0的矩阵不可逆,而不为0的矩阵则可逆。那么,代表面积的行列式是如何与线性变化的可逆性相结合的呢?
我们需要理解线性变换的几何意义。设定一组线性无关的矢量为列向量,那么它们张成的N维体积不为零,行列式可以为其赋值。经过线性变换A后,新矢量的形式如下:
值得注意的是,A为N*N的矩阵,而矢量则为列向量。
变换前,N维体的体积为:
变换后,N维体的体积则为(此等式说明了几何意义如何定义矩阵乘法,即N*N矩阵A与其他N个列向量组成的N*N矩阵的乘法):
若A的行列式不为零,说明变换后的N维体积不是零;结合线性无关性与体积的性质,我们可以得出结论:
若A的行列式不为零,则A能将一组线性无关的矢量映射为另一组线性无关的矢量,表明A是可逆的(即一对一映射,保持性质,KERNEL为{0})。
反之,若A的行列式为零,则其会将一组线性无关的矢量映射为线性相关的矢量。
若A的行列式为负数,则会改变原N维体积的方向。
从线性无关到线性相关的转变中,信息的丢失(例如退化为共线或共面)使得这一变换显然不可逆。线性是否无关与所张成N维体积有直接关系,而体积值又与A的行列式相对应。这建立了A的行列式与其可逆性之间的几何关系。
举个例子,假设A为3维矩阵。若映射前有一组三个线性无关的矢量,它们所张成的体积不为零;映射后对应的新矢量仍能张成平行六面体,此时

