e的ln2次方等于多少 e的ln2的次方
探索自然数倒数和的奥秘
让我们从一个有趣的例子开始,逐步揭开自然数倒数和的神秘面纱。我们来看看小明和他的火腿肠吧。
假设小明对火腿肠情有独钟。第一天,他独享一根火腿肠。自第二天起,天天有新的朋友加入,火腿肠也开始分给更多的人。假如每天火腿肠按人数均分,请问他在以后日子里能累计吃到10根火腿肠吗?

乍看之下,似乎不可能达到,因为随着分享人数的增加,每个人分到的火腿肠会越来越少,趋近于0。那么,真的能够累计到10根吗?或许连2根都显得很困难。
让我们细细分析:
事实上,累计达到2根火腿肠并不是难事。第一天,小明吃了一根。第二天,他吃了1/2根,第三天是1/3根,第四天则是1/4根。我们可以将这些相加:

1 + 1/2 + 1/3 + 1/4 = 25/12,这已经超过了2根。
那么,累计吃到超过3根火腿肠会怎样呢?
如果逐项计算,每一项的计算会显得繁琐。更高效的方法是用估算技巧来解决这个问题:
我们可以将数列的和分组来估计:
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + … + 1/16
可以按照如下方式进行分组:
1 + (1/2) + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) + (1/9 + 1/10 + … + 1/16)
≥ 1 + (1/2) + (1/4) × 2 + (1/8) × 4 + (1/16) × 8 = 3
这意味着,在第16天,小明累计吃到的火腿肠总数将超过3根。
根据这个估算,我们可以进一步推算小明累计吃到10根火腿肠的天数:
数列的和:
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + …
通过分组处理,可以得到:
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + … > 1 + m/2
为了使其总和超过10,我们需要 m > 18。至少需要18个括号分组,那么最终的项数应该在接近多少呢?
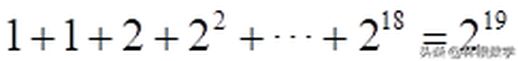
约为524,288项,这显然是一个庞大的数目。实际计算时,也可以通过对2的19次方进行估算:
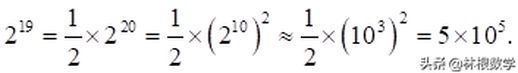
由于估算不完全准确,实际可能更少。至今还没有一个精确的方法来确定准确的项数。
我们可以借助图形化方法来理解:
绘制 y=ln(1+x) 和 y=x 的图像可以帮助我们理解:
x > ln(1+x)
我们可以得出:
S=1 + 1/2 + 1/3 + … + 1/n > ln(1+1) + ln(1+1/2) + ln(1+1/3) + … + ln(1+1/n)
= ln(2) + ln(3/2) + ln(4/3) + … + ln((n+1)/n)
= ln(2*3/2*4/4*…*(n+1)/n) = ln(1+n)
实际上,还可以证明:
S=1 + 1/2 + 1/3 + … + 1/n
这表明 1 + 1/2 + 1/3 + … + 1/n 与 ln(n) 是接近的,虽然两者之间存在常数差距 C,欧拉常数 C 约为 0.1209……,但至今尚未确定它是否为有理数。
调和级数的求和和欧拉常数在高等数学中具有重要作用。接下来,我们来探讨另一个有趣的问题。
2. 小红非常喜欢披萨饼。第一天她独享一只披萨,但之后的每一天,按天数的平方递增人数(即第n天有n²人)。若每个人均分披萨,小红最终能累计吃到超过两只披萨吗?

乍一看,这个问题似乎与调和数列的求和方法相关。我们来看看:
小红的披萨数量:
1 + 1/(2×2) + 1/(3×3) + 1/(4×4) + … + 1/(n×n)
可以分组如下:
1 + [1/(2×2) + 1/(3×3)] + [1/(4×4) + 1/(5×5)] + …
我们发现分母的增长不规律,无法用之前的方法进行估算。
我们尝试逐项计算:
设 S(n) = 1 + 1/(2×2) + 1/(3×3) + 1/(4×4) + … + 1/(n×n)
计算得到:
S(1) = 1
S(2) = 1 + 1/(2×2) = 5/4 = 1.25
S(3) = 1 + 1/(2×2) + 1/(3×3) = 49/36 ≈ 1.36
S(4) = 1 + 1/(2×2) + 1/(3×3) + 1/(4×4) ≈ 1.42
S(5) = 1 + 1/(2×2) + 1/(3×3) + 1/(4×4) + 1/(5×5) ≈ 1.46
可以看出,随着 n 的增加,增加的幅度变小,表明这个数列是有界的。
实际上,S(n) 满足以下不等式:
S(n)
= 1 + (1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + … + [1/(n-1) - 1/n]
= 2 - 1/n
显然,无论 n 如何,2 - 1/n 总是小于2。这表明,小红按这种方式累计的披萨不会超过两块。
小红能否在这种情况下吃到超过一只蛋糕呢?这个问题和之前的问题类似,但不同之处在于增量和有界性的讨论。
小英对蛋糕的喜爱不亚于对披萨。她的情况是每天来的人数按立方递增,是否会比前面的问题复杂?
按之前的方法,虽然我们知道数列是单调有界的,但至今对其极限值的精确表达仍无确切答案。解决此问题需要深入研究,探索与已知超越数的关系等。

