三角函数恒等变换公式 高中三角函数所有公式大全

三角函数在数学中占据了核心地位，特别是关于任意角度的三角恒等变换公式，这些内容是我们学习的重点。

本文将详细探讨三角公式的推导过程，特别是如何通过各种方法来证明这些公式的有效性。

我们需要了解两角余弦差公式的推导。这部分内容的核心工具是

向量

，因此了解向量的运算（包括加减法和数量积运算）是必要的。

说明：两个向量的点乘等于这两个向量模的乘积与夹角余弦值的乘积。两个向量的数量积也等于它们对应坐标的乘积之和。

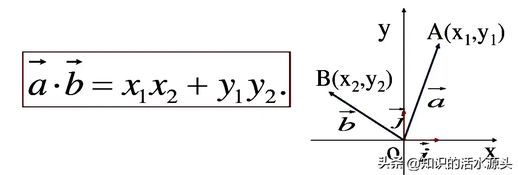
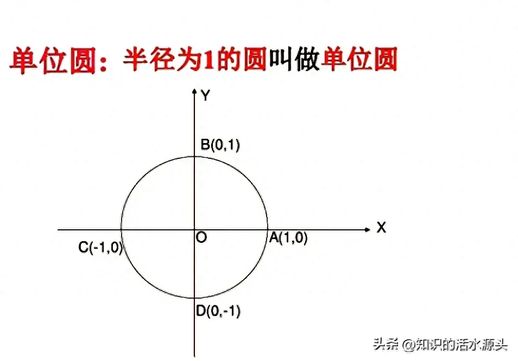
上述两个要点是推导余弦差公式的基础，接下来我们将使用

单位圆

来深入研究这个公式。

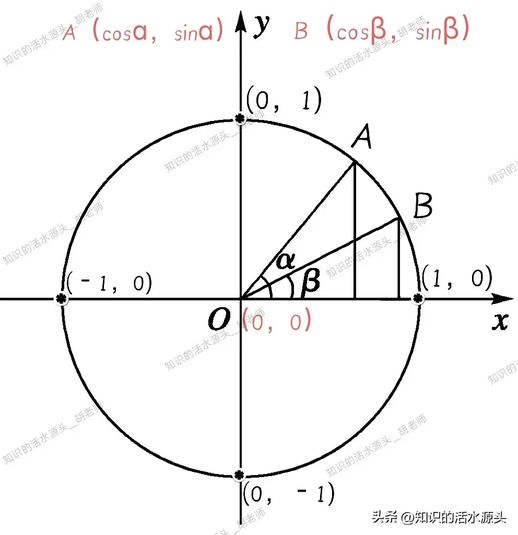
考虑两角和与差的余弦公式：

在单位圆上设∠XOB＝β，∠XOA＝α，则∠AOB＝α－β。由此，点A的坐标为（cos α，sin α），点B的坐标为（cosβ，sinβ），其中O为坐标原点（0，0）。

从这些坐标出发，可以得到向量

OA

OB

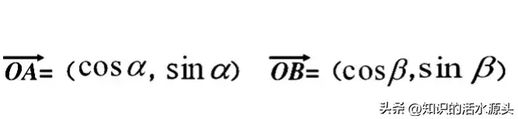
使用向量的数量积运算，将其转化为

坐标运算

后，我们可以得到cos（α－β）的表达式，从而推导出两角余弦差的运算公式。

结合两种点乘运算形式，我们可以得出所需结果。接下来，我们将讨论余弦两角和公式的推导。

注释：推导余弦和公式时，可以借助余弦差公式。如果令β＝－β，那么cos（α＋β）＝cos[α－（－β）]，结合诱导公式即可得到余弦两角和公式。

和差积余弦公式可以表示如下：

接下来是两角和与差的正弦公式：

正弦公式的推导可以通过两角差的余弦公式完成。我们可以将余弦转换为正弦，

转换时需要考虑奇偶性以及象限符号

根据这些步骤，我们可以得到两角和的正弦公式。而对两角差的正弦公式的推导，则可以使用两角和的正弦公式。通过令β＝－β，我们可以得到sin[α＋（－β）]＝sin（α－β），再根据两角和的正弦公式展开即可。

以上讨论帮助我们整合了两角和与差的正弦公式，如下所示。

探讨二倍角公式：

正弦的二倍角公式可以通过两角和的正弦公式推导，令

β＝α

。对于余弦的二倍角公式，我们同样可以使用两角和的余弦公式，令

β＝α

结合

sin²α＋cos²α＝1

，我们可以进一步转化上述二倍角公式，如下所示：

还有降幂扩角公式：

通过

正弦和余弦的二倍角公式

的转换，我们可以得出降幂扩角公式。

升幂缩角公式：

这些公式也是通过倍角公式进行变换，只需移项即可得到。

半角公式：

在推导半角公式时，我们可以通过将正弦和余弦的二倍角公式中的α用2α替换，以α/2代替α来进行。

今天的内容到此为止，希望大家能通过这些推导公式加深对三角函数的理解。练习题在下方，请大家完成练习以巩固所学知识。

欢迎不同观点的朋友留言讨论，供大家参考。