30的因数有几个 30的因数有几个数字

因式分解是解决二次方程的有效方法之一。今天，我们将通过几个具体的例子来深入探讨这个过程。我们考虑一个二次函数f(x)=x²+6x+8，并通过图像直观地理解它。想象一下这条抛物线与x轴交于两处，接下来我们需要找到这两个交点的具体位置。

要解这个问题，首先需要将方程f(x)=0转化为一个简单的形式，即x²+6x+8=0。尽管这看似简单，但x²的存在使得问题变得稍微复杂，因此我们需要进行因式分解。目标是将x²+6x+8表示为(x+a)(x+b)的形式。

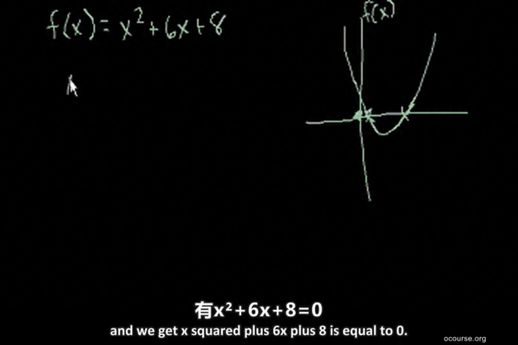
接下来，我们需要找出两个数，使得它们的和为6，积为8。8的因数有1, 2, 4, 8，其中1和8的和为9，不符合要求，但2和4的和正好是6。由此，我们可以将x²+6x+8因式分解为(x+2)(x+4)=0。

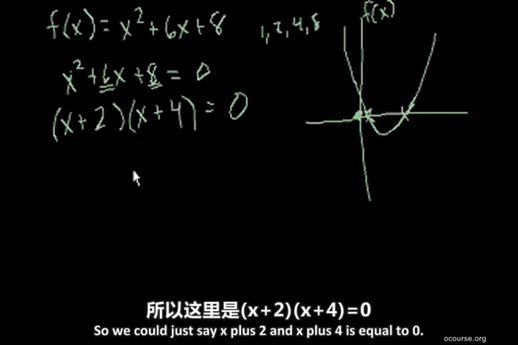
当两个因式相乘为0时，至少有一个因式必须为0。我们得到x+2=0或x+4=0，解得x=-2和x=-4。你可以将这些值代入原方程，验证它们的正确性。这里我们简化了步骤，你可以自己检查-2和-4的结果。

(-2)²+6*(-2)+8=0，这表明解的正确性。接下来我们探讨一个稍微不同的问题，即f(x)=2x²+20x+50与x轴的交点。设定f(x)=0，得到方程2x²+20x+50=0。为了简化计算，我们将方程两侧都除以2，得到x²+10x+25=0。

现在你可以尝试将x²+10x+25因式分解为(x+a)²的形式。25的因数是1, 5, 25，其中5和5的和为10，因此分解式为(x+5)(x+5)=0，这意味着x+5=0，解得x=-5。

这个方程的解只有一个，因为抛物线与x轴只相切一次。如果你将(x+5)(x+5)展开，你会发现它等同于原方程x²+10x+25，从而验证了解的正确性。

让我们再看一个例子：解x²-x-30=0。我们需要找出两个数，使得它们的和为-1，积为-30。通过分析因数对，我们发现-6和5的差为1，且-6×5=-30。由此，我们可以将方程因式分解为(x-6)(x+5)=0。

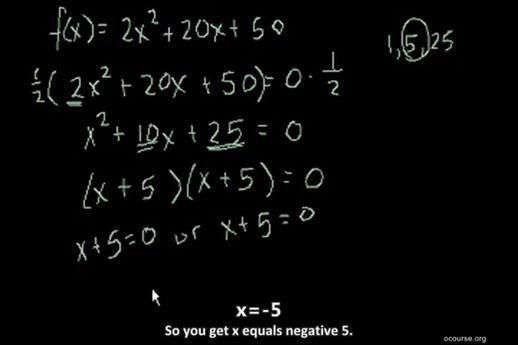
这时我们得到x=6和x=-5。虽然这个过程看起来复杂，但通过练习会变得更加熟练。你可以尝试类似的题目，逐步提高自己的解题能力。更多讲解和示例请继