三角形中心是什么 三角形中心是什么点

了解三角形的四个核心点是掌握几何基础的重要一步。这四个点包括重心、垂心、内心和外心。每一个点都有其独特的性质和应用场景，让我们逐一探讨这些关键的几何概念。

重心是三角形中线的交点。中线指的是从一个顶点到对边中点的连线。因为中线始终位于三角形内部，所以重心也一定在三角形内部。一个关键的性质是：重心到顶点的距离是到对边中点距离的两倍。举例来说，如果中线AD，重心G把AD分成AG和GD，其中AG是GD的两倍，这样AD被分成了三份，AG占三分之二，GD占三分之一。这一性质同样适用于三角形的所有中线。

重心还有一个重要的特性，即它将三角形的面积分成六个相等的小三角形。因为每条中线将三角形分成两个底和高相等的小三角形，所以这些小三角形的面积也相等。由此，我们可以得出一个结论：通过中线划分的每个小三角形，其面积都等于大三角形面积的六分之一。

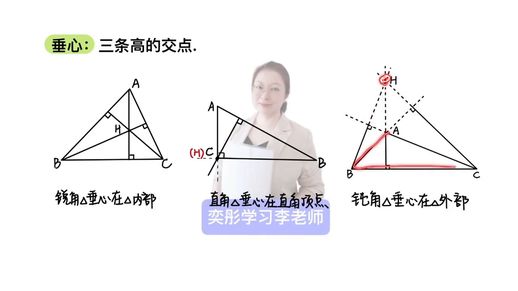
接下来是垂心，它是三角形三条高的交点。垂心的位置取决于三角形的类型：对于锐角三角形，所有的高都在三角形内部，因此垂心也在内部；对于直角三角形，垂心正好位于直角顶点；对于钝角三角形，垂心则位于三角形的外部，因为钝角三角形的高线需要延长到外部。

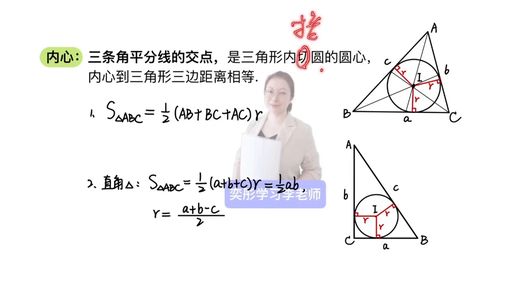
内心是三角形三条角平分线的交点。它的主要特性是，内心到三角形的每一条边的距离相等。内心所形成的圆称为内切圆，这个圆和三角形的三条边相切。由于角平分线的性质，内心也正是这个内切圆的圆心。

我们还有两个重要的结论关于内心。首先是内切圆的面积计算，虽然不同的记号可以用来表示，但关键在于了解三角形的面积与内切圆的半径之间的关系。具体地，通过已知的三角形的边长和内切圆的半径，可以计算出三角形的面积。对于直角三角形，面积可以通过两个直角边相乘后除以二来求得，这样的计算方法与内心的半径相关联。

最后是外心，它是三角形三条中垂线的交点。外心的特点是：在锐角三角形中，外心位于三角形内部；在直角三角形中，外心正好是斜边的中点；而在钝角三角形中，外心位于三角形的外部。外心所在的圆称为外接圆，它通过三角形的三个顶点，其圆心到每个顶点的距离相等。

虽然中心的概念在正三角形中表现得尤为特殊，所有四个点——重心、垂心、内心和外心——在任何三角形中都存在，并且每个点都有其独特的几何意义。希望这篇文章能帮助您更好地理解这四个核心点及其性质。

如果对这些几何知识还有疑问，欢迎在评论区留言，我们可以进一步探讨。了解这些基础知识是几何学习的第一步，掌握它们会让你在更复杂的几何问题中游刃有余。