抛物线标准方程 y2=2px图像及性质

导言

继讲解了椭圆与双曲线的标准方程及几何性质后，本节我们将深入探讨抛物线及其标准方程。未曾阅读前文者，可参阅作者过往发布的文章。

抛物线的定义

了解抛物线的第一个步骤即明确其定义。但我们先观察其图像：

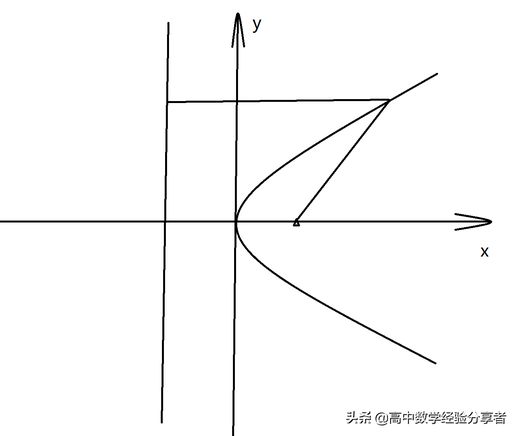
数学定义：

平面内与一点 F 和一条不通过 F 的直线 l 等距离的点的轨迹称为抛物线。

其中，点 F 称为抛物线的焦点，直线 l 称为抛物线的准线。

分析：

根据这一定义，焦点和准线是图像元素中最核心的，而等距离关系直接促成了抛物线的标准方程。

抛物线的标准方程

根据定义，我们可以推导出多种标准方程。由于焦点可能位于平面中的以下四个位置，因此可得到四个标准方程：

• x 轴正半轴
• y 轴正半轴
• x 轴负半轴
• y 轴负半轴

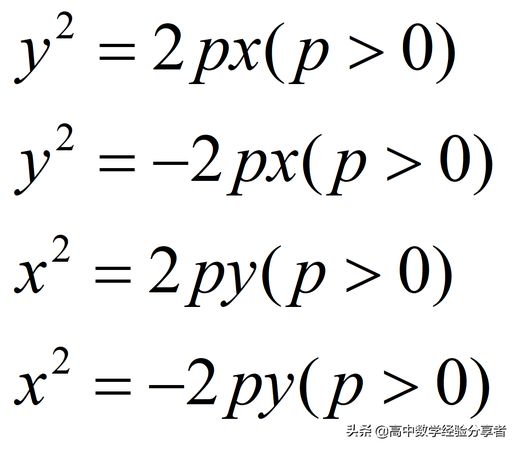
以上为由焦点位置推导出的四种标准方程。

对应于这些方程的函数图像为：

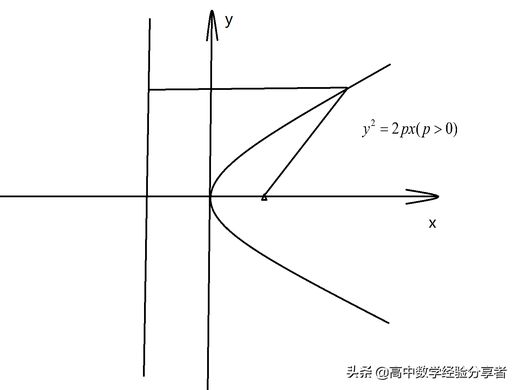
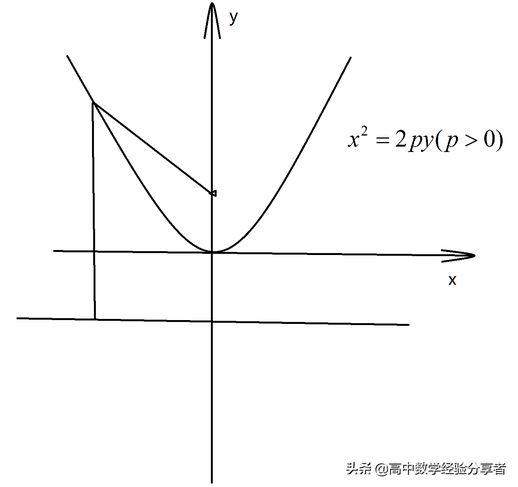
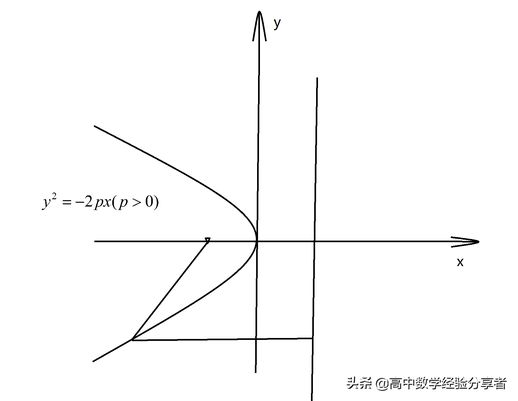
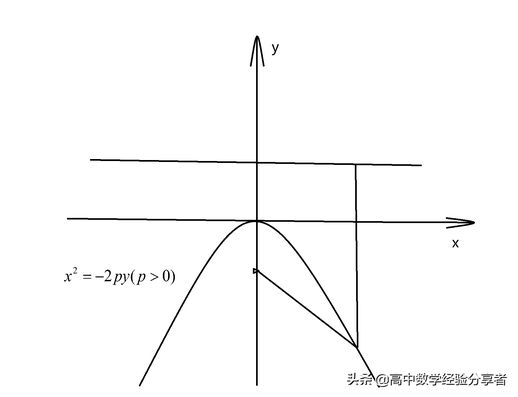
上述即为抛物线的四种方程，读者须熟记并学会甄别。

抛物线方程分析

不同焦点位置对应不同的坐标：

具体选取何种焦点坐标取决于实际位置。

不同准线位置对应不同的方程：

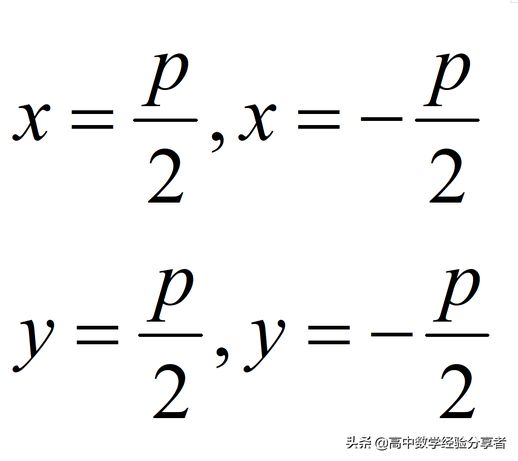
同样地，应根据准线所在位置选取对应的方程。

注：

如有疑难，欢迎留言提问。若有高中解题经验分享需要，亦可与作者联系。

关注！关注！关注重要的事情说三遍！