概率密度函数怎么求 求概率密度的两种方法
从随机实验到随机变量:用数字刻画不确定性
通信-随机过程系列第2篇
虽然随机实验的结果都有明确的含义,但直接使用这些结果进行数学分析往往很不方便。例如,抛硬币的结果是“正面”或“反面”,这对数学计算并不友好。
让我们先来看一个例子:假设一个喷泉每隔91分钟喷发一次,你随机抵达喷泉并停留20分钟,那么你能看到喷泉喷发的概率是多少呢?

为了更方便地分析这类问题,我们可以用数字或数值序列来表示随机实验的结果。例如,可以用数字“1”代表硬币的“正面”,用数字“0”代表硬币的“反面”。这种将随机实验结果与数字对应起来的过程,就称为用随机变量表达。
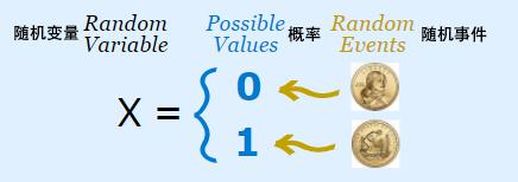
图1展示了抛硬币实验中,结果与随机变量之间的对应关系。
具体来说,假设一个随机试验的样本空间为S,随机实验的结果为s(s∈S)。我们可以定义一个函数X(s),它的定义域为样本空间S,值域为实数的子集。这个函数X(s)就被称为随机变量。
图2更清晰地展示了随机变量的概念。通过引入随机变量,我们在概率和样本空间之间建立了联系,使得数学计算更加方便。
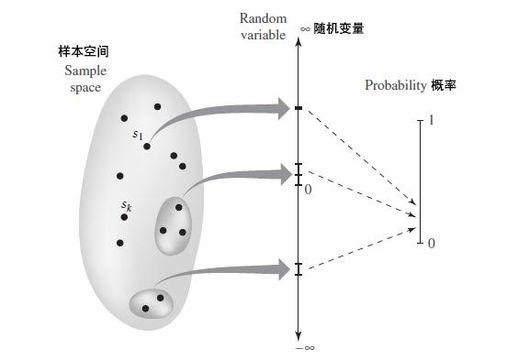
图2 随机变量的概念
使用随机变量的优势在于:无论随机实验本身的形式如何,我们都可以通过分析具体数值的概率来研究问题。随机变量可以是离散的,只能取有限个值,例如抛硬币实验中的随机变量;也可以是连续的,可以取某个区间内的任意实数,例如表示噪声电压幅值的随机变量。随机变量还可以是复数,但复随机变量通常被视为两个实随机变量组成的向量。
举例1:抛3枚硬币,出现几个正面?
在这个例子中,我们可以定义随机变量X为“正面出现的次数”。X可能的取值为0、1、2、3,分别对应所有硬币都是反面、出现1个正面、出现2个正面和出现3个正面。样本空间为{0, 1, 2, 3}。
需要注意的是,此时每种结果出现的概率不再相等。抛掷3枚硬币共有8种可能结果:

图3 抛掷3枚硬币的8种结果 (H代表正面,T代表反面)
从图3可以看出,只有1种结果包含3个正面,3种结果包含2个正面,3种结果包含1个正面,1种结果没有正面。因此:
- P(X=3)=1/8
- P(X=2)=3/8
- P(X=1)=3/8
- P(X=0)=1/8
举例2:同时抛掷2个骰子,点数之和是多少?
在这个例子中,我们可以定义随机变量X为“两个骰子点数之和”。
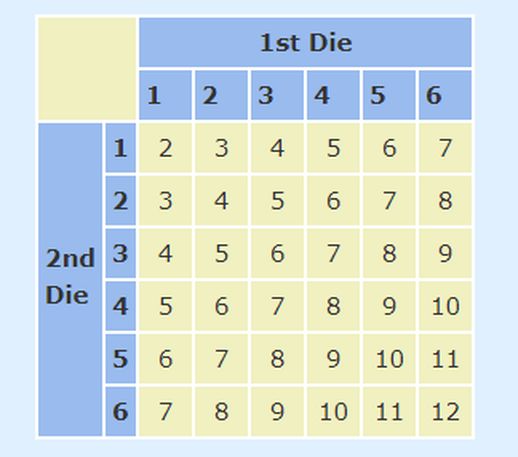
图4 抛掷2个骰子的36种结果
图4展示了抛掷2个骰子可能的36种结果。样本空间S为{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}。
我们可以统计每个点数和出现的次数,并计算其概率:
- 2只出现1次,所以P(X=2)=1/36;
- 3出现2次,所以P(X=3)=2/36=1/18;
- 4出现3次,所以P(X=4)=3/36=1/12;
- 5出现4次,所以P(X=5)=4/36=1/9;
- 6出现5次,所以P(X=6)=5/36;
- 7出现6次,所以P(X=7)=6/36=1/6;
- 8出现5次,所以P(X=8)=5/36;
- 9出现4次,所以P(X=9)=4/36=1/9;
- 10出现3次,所以P(X=10)=3/36=1/12;
- 11出现2次,所以P(X=11)=2/36=1/18;
- 12出现1次,所以P(X=12)=1/36;
问题:两个骰子点数之和为5、6、7或8的概率是多少?
换句话说,我们需要计算P(5≤X≤8) 的值。
由于随机变量X是离散的,所以P(5≤X≤8)=P(X=5)+P(X=6)+P(X=7)+P(X=8)=(4+5+6+5)/36=20/36=5/9
同样地,表示特定时刻噪声电压幅度的随机变量是连续的,因为它理论上可以取正负无穷之间的任意值。
以抛硬币实验为例,我们可以用下图来描述:

图5 硬币抛掷实验的随机变量
其中,x=0代表硬币反面朝上,x=1代表硬币正面朝上,P[X=x]表示结果为x的概率。图中的两个权重为1/2的delta函数分别代表抛硬币的两种可能结果。
总而言之,随机变量可以是离散的,也可以是连续的,它为我们分析和计算随机事件的概率提供了更便捷的工具。
从离散到连续:深入理解概率分布
我们先回顾一下两种不同类型的数据:
- 离散数据: 只能取特定值,例如整数 1、2、3、4、5。
- 连续数据: 可以在一个范围内取任意值,例如身高。
我们已经了解了离散随机变量的例子,现在我们将重点关注连续随机变量。
均匀分布 (矩形分布)
在均匀分布中,随机变量落在区间 [a, b] 内任何点的概率都是相等的。与离散随机变量不同,连续随机变量在区间内有无限多个可能取值。
为了保证所有可能结果的概率之和为1,均匀分布的概率密度函数呈现为一个矩形:
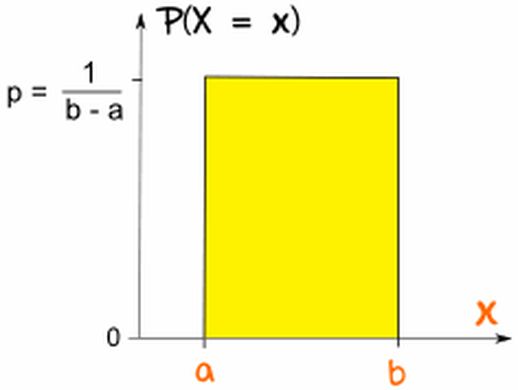
图1: 均匀分布
由于矩形面积代表总概率 1,我们可以推导出概率密度函数:
矩形面积 = 1 = p × (b - a)
p = 1 / (b - a)
用数学语言表达:
当 a ≤ x ≤ b 时,P(X = x) = 1 / (b - a)
其他情况下,P(X = x) = 0
喷泉问题:
假设一个喷泉每隔一段时间喷发一次,最长间隔为 91 分钟。你随机到达喷泉,等待时间不超过 20 分钟的概率是多少?
答案:
你等待时间不超过 20 分钟的概率,相当于随机变量(等待时间)落在 0 到 20 分钟这个区间内的概率。由于喷发时间服从均匀分布,概率密度为:
p = 1 / (91 - 0) = 1 / 91
等待时间不超过 20 分钟的概率为:
p 20 = (1 / 91) 20 ≈ 0.22
这意味着你有大约 22% 的概率在到达后 20 分钟内看到喷泉喷发。
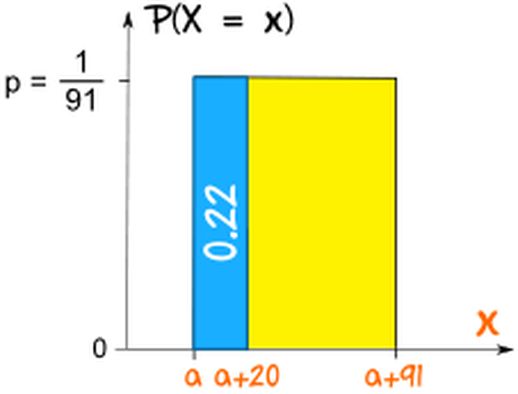
图2: 喷泉问题的均匀分布
累积分布函数 (CDF)
除了概率密度函数,我们还可以用累积分布函数 (CDF) 来描述概率分布。CDF 表示随机变量取值小于或等于某个特定值的概率。
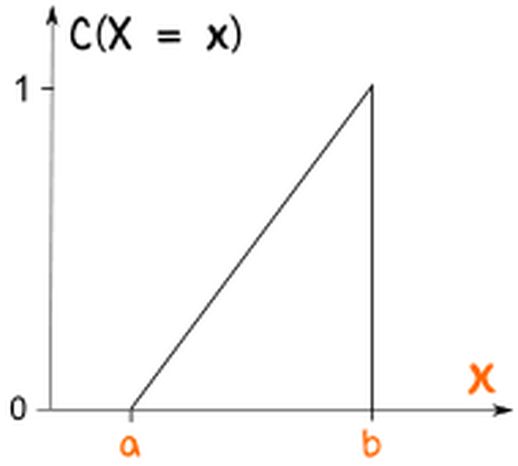
图3: 累积均匀分布
例如,在喷泉问题中,等待时间不超过 20 分钟的累积概率约为 0.22。
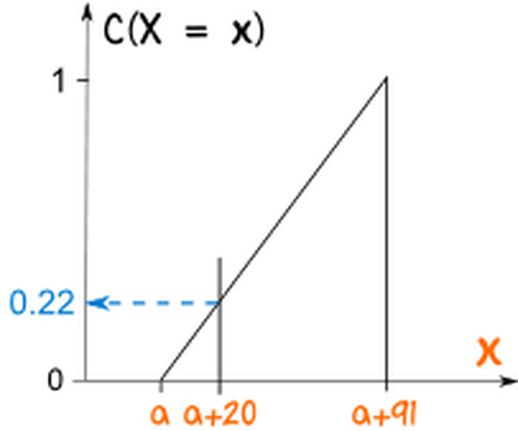
图4: 使用 CDF 计算概率
用数学语言表达:
FX(x) = P(X ≤ x)
CDF 有以下特性:
1. 0 ≤ FX(x) ≤ 1
2. FX(x) 是一个单调不减函数.
3. 如果 FX(x) 可微,则其导数为概率密度函数 fX(x).
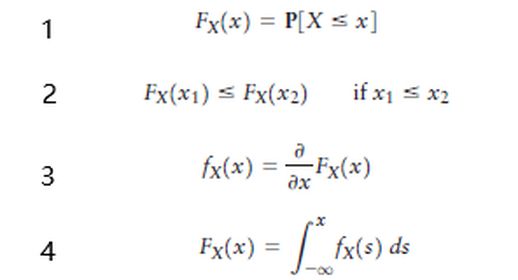
图5: 概率分布函数
概率密度函数 (PDF)
概率密度函数 (PDF) 描述随机变量在某个特定值的“密度”。理解 PDF 的关键在于,它本身不是概率,而是概率的变化率。
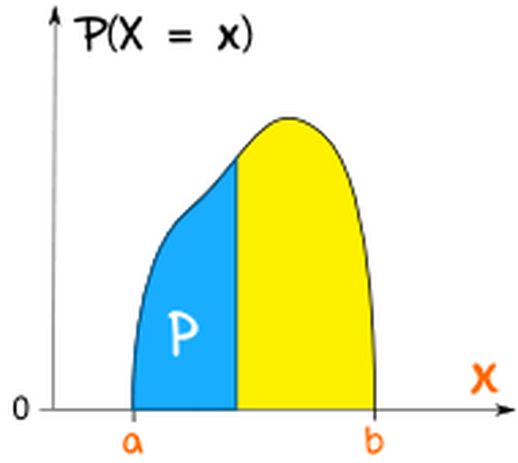
图6: PDF
PDF 有以下特性:
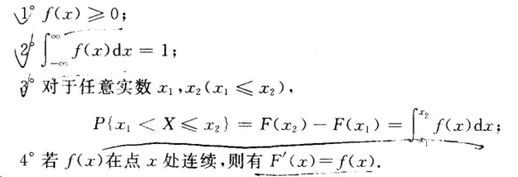
图7: PDF 的特性
随机变量 X 落在区间 [x1, x2] 内的概率等于该区间上 PDF 曲线下的面积:

正态分布
正态分布是最重要的连续概率分布之一。标准正态分布的随机变量通常用 Z 表示,其图形是一个对称的钟形曲线。
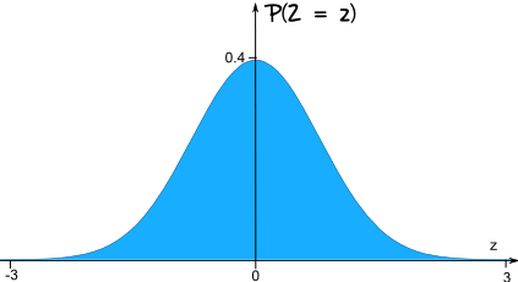
图8: 正态分布曲线
我们可以使用标准正态分布表查找 Z 落在特定区间内的概率。例如,要查找 P(0 < Z < 0.45),即 Z 落在 0 到 0.45 之间的概率,我们可以在标准正态分布表中找到对应于 0.45 的概率值,约为 0.1736。
P(0 < Z < 0.45) = 0.1736。 分析随机变量的统计量
随机变量由于取值随机而捉摸不定,但可以通过提取确定的统计量来把握其特征。
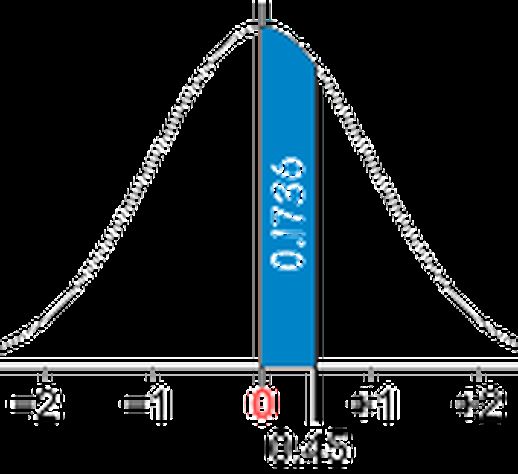
图 14:计算概率
随机变量的矩
总体而言,随机变量的 N 阶矩 定义为:

一阶矩便是随机变量的 均值 (MEAN),二阶矩则为 功率。
随机变量的中心矩
当随机变量减去其均值后,再求得的 N 阶矩即为 N 阶中心矩。
一阶中心矩永远为零,二阶中心矩则被称为 方差。

方差是一个极其重要的统计量,反映了随机变量与均值的偏离程度。
对于均值为零的信号,方差等于信号的功率。对于非零均值信号,方差等于功率减去均值的平方。


