列举生活中的大数
最大公约数的知识点
2018 年7月22 日星期日
五年级的数学知识“因数与倍数”及其后续知识,难住了很多小朋友。大体除了在对待方式和学习态度上有差异,这部分内容所涉及的概念较多、其中的关系较为隐晦、而且与小朋友们所熟悉的日常生活联系少,这也值得探索的原因。抽象思维的特征是运用概念来进行思考、判断和推理。对于有困难的同学来说,说明你的思维正处于一个艰难的转型期,如果能熬过去,就会豁然开朗。选取这个话题,也是我一时兴起,随性而为。希望对小朋友们有所帮助。
谈到“最大公约数”,你首先能想到什么?
……
……
……
……
……
……
如果你的答案是“短除法”,说明我和你想到一块去了。对此,你应该充满自信和欣慰。求最大公约数的方法正是今天话题的核心。首先让我们寻根溯源,看看“最大公约数”是哪根藤上结出的瓜。
回顾我们曾经做过的自然数的除法——做了大量且重复繁琐的除法,你应该认可以下的发现。在此之前,我们最好先将0从自然数的集合中剔除掉:0总是扮演一个“坏蛋”角色——它不能做除数、不能做分母、不能做比的后项、也不能做自然数的最高位,无论走到哪里,都会“捣乱”;0混入自然数的集合中,一直存在争议,许多数学“大牛”对此都持保留意见。最重要的是,我们不想再和这个“坏蛋”纠缠太多了。
自然数的除法分为三种情况:
1.商是整数且没有余数,比如:6÷2=3;
2.商是有限小数,比如:10÷8=1.25;
3.商是无限循环小数,比如:1÷7=0.142857 142857……。
显然,这是在数系由自然数扩展到小数的情况下进行的讨论。所谓“自然数的除法”,我们只是对被除数、除数有所限制,而不是对其结果有所限制。这样的话,2、3应该合并为“有余数的除法”。
在上述三种除法中,第1种是最完美的:被除数、除数和商都是自然数,且没有余数。如果除数和商还是一位数的话,就是我们最喜欢的“表内乘除法”。对于这种完美的除法,我们给它起个名字叫做“整除”。而“整除”这个“根”上,将会长出“因数与倍数”等一系列茁壮的茎和丰硕的果实。如果你在学习上也不“忘本”的话,你也会成为一个受人尊敬的人。
“整除”生下两个孩子:因数和倍数。6÷2=3,我们说:6能被2整除,或者2能整除6;我们定义为:6是2的倍数,2是6的因数。因数和倍数就像“爸爸”、“妈妈”、“儿子”、“女儿”……这些概念一样,表示的是一种关系,而不是具体事物的名称。“甲是爸爸”和“6是倍数”的错误是一样的,应该说“甲是谁的爸爸”、“6是谁的倍数”。你应该能理解:没有人敢给自己取名叫“爸爸”。
从那时起,“因数”与“倍数”蓬勃发展,衍生出许许多多“悲壮”的东西。我们稍微用一张图示来看看它们,从中找到一种“弹指间灰飞烟灭”的虚妄感觉。
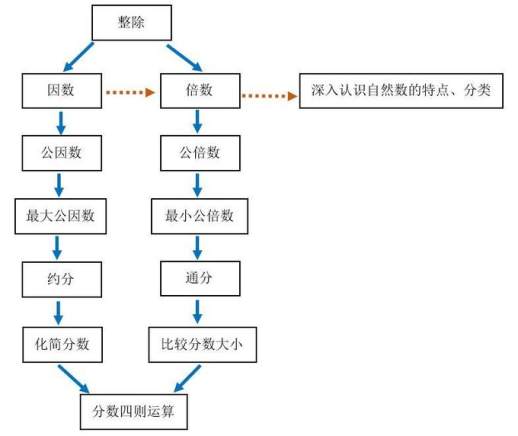
深入理解自然数,为分数四则运算奠定基础,这是这些知识的重要目的和归宿。“公约数”之所以多了一个“公”字,是因为研究角度发生了变化:由寻找一个自然数的因数变成了寻找两个或更多自然数的相同的因数。“最大”公约数说明,在一众“公约数”中,鹤立鸡群的“老大”才是最突出、最有意义的。求取两个或多个自然数的最大公约数,基于这些原生概念,又有新的思维方法。不要过分自恋于已经知道的知识和掌握的方法,在我们还没有提升到一个新的思维层次的时候,我们无法准确、全面、深入地了解自己的幼稚。这句话也许会成为你阅读本文最大的收获。
以下的做法,目的是“删繁就简,抓住主要矛盾”。
(一)符号约定。8和12的最大公约数,记为:(8,12)=4;最小公倍数记为:[8,12]=24。一个用圆括号,一个用方括号,数字间以逗号隔开。计算机里又有以下表示:最大公约数:gcd(8,12)=4,最小公倍数:lcm(8,12)=24。“gcd、lcm”分别是英文“最大公约数、最小公倍数”的单词的首字母,计算机里常用其作为函数名或命令名。
(二)情况简化。求多个自然数的最大公约数或最小公倍数的问题都可以转化为求两个自然数的gcd或lcm。例如:
(8,12,16)=((8,12),16)=(4,16)=4
[8,12,16]=[[8,12],16]=[24,16]=48
你理解其中的化归思路吗?如果要求3个自然数a、b、c的最大公约数(最小公倍数同),我们可以先随便拿出其中的两个数求取最大公约数g1,然后再用g1与第三个数再次求取最大公约数,设为g,就是这3个自然数的最大公约数。
(a,b,c)=((a,b),c)=(a,(b,c))=((a,c),b)
(a,b,c)=((a,b),c)=(g1,c)=g
我们只需重点讨论如何求取两个自然数的最大公约数就可以了,拓展时要做的就是:再来一遍、再来一遍、再来一遍……
方法一:列举法
有时,我不认为这是求最大公约数的方法,它用来解释概念。
(8,12)=?
①列举8的所有因数:1、2、4、8;
②列举12的所有因数:1、2、3、4、6、12;
③列举公约数:1、2、4;
④找出最大公约数:4。
(8,12)=4。
仅此一例,聪明的你就会理解一系列概念。
方法二:短除法
下图是人教版五年级《数学》下册第56页、61页的课外知识介绍:
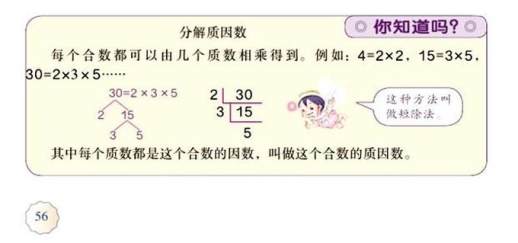
人教五数下册56页

人教五数下册61页
显然,这是重要的,老师们会将其重新搬回课堂中。此处不再赘述。我们将重点放在“短除法”的理解上。
对比一下除法竖式和 三种方法求最大公因数,哪种更高效?
你是否好奇过,除了列举法,还有哪些方法可以求最大公因数?本文将介绍两种更简洁的方法:短除法和辗转相除法。
短除法:省略中间步骤,快速求解
短除法可以看作是竖式除法的简化版,它省略了乘积、求差、比较余数等步骤,直接写出商。如下图所示,短除法将多步竖式除法浓缩成一步,大大提高了效率。
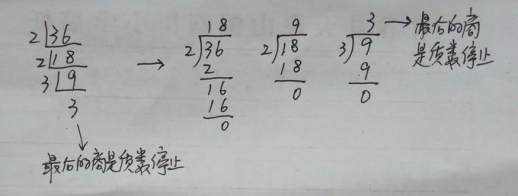
利用短除法求最大公因数,实际上是对两个数进行质因数分解,并将相同的质因数排列在一起。例如,求(24, 36)的最大公因数:
24 = (2×2×3)×2
36 = (2×2×3)×3
可以看出,24和36相同的质因数部分是2×2×3,即为它们的最大公因数12。
短除法也有一定的局限性。如果被除数很大,心算能力较弱的小朋友可能需要借助竖式除法来计算商。
辗转相除法:古代智慧的结晶
辗转相除法源于我国古代的“更相减损术”,它通过不断进行除法运算,直到余数为0,此时最后一步的除数即为最大公因数。
例如,求(77, 21)的最大公因数:
77 ÷ 21 = 3……14
21 ÷ 14 = 1……7
14 ÷ 7 = 2……0
(77, 21)的最大公因数为7。
相比之下,辗转相除法比短除法更加简洁高效,尤其是在处理大数时优势更加明显。
算法的力量:从最大公因数到“NP难题”
也许你会认为这两种方法都不够高效,但在计算机科学领域,算法的选择至关重要。例如,判断一个大数是否为质数是一个被称为“NP难题”的经典问题,即使是计算机也难以在有限时间内解决。
在这种情况下,如果使用列举法或短除法编写代码,程序的运行效率会非常低。而使用辗转相除法,则可以大大简化代码,提高程序的运行效率。

结语
数学的世界充满了奇妙与乐趣,探索不同的解题方法就像在旅行中发现新的风景一样令人兴奋。希望小朋友们保持好奇心,不断探索,在学习数学的过程中收获知识与快乐!

