建模是什么

"模型"：从橘猫、模特到公式， 一文读懂模型的真谛

近年来，"模型"一词可谓炙手可热，与"闭环"、"赋能"等热门词汇不相上下。词汇本身无过错，错的是使用不当。今天，我们就来深入浅出地聊聊"模型"的含义、现状以及错误示范。

根据维基百科的定义，模型是指对某个实际问题或客观事物、规律进行抽象后的一种形式化表达方式。

重点来了：抽象！模型的意义在于简化认知成本，帮助我们拨开迷雾，抓住事物的本质。

以胖橘猫为例，在爱猫人士眼中，自家橘猫千姿百态、独一无二。但在不爱猫的人眼中，橘猫的特点可以概括为"橘色"和"胖"。如果让这个人画一只橘猫（"建模"），他可能会画出类似加菲猫的形象（这引出下文将要讨论的，引入不完整或错误的特征变量会导致模型解释力不足）。

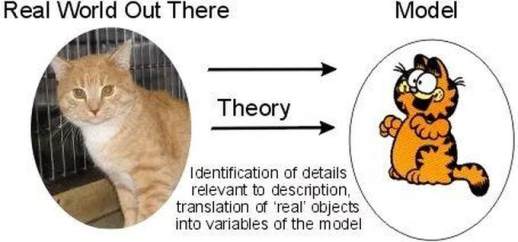
"模型"的英文是"model"，与"模特"同义。 模特的身材通常符合大众审美，能够很好地展示服装的特点， 这是否是对客观事物（服装）的一种抽象化表达呢？人们的注意力可以集中在服装上（这也解释了为何许多模特走秀时不苟言笑）。

在我看来，优秀模特应该能够驾驭不同风格品牌的服装，例如我很欣赏的刘雯，既能走高端品牌秀，也能完美诠释本土品牌，例如Dazzle、鄂尔多斯以及运动品牌Puma。

（左：Dazzle 右：维密）

你可能会问：建模会不会很难？

答案是：不会！你从小学就开始接触建模了！ 你还记得解一元一次方程吗？那就是一种简单的建模。

我曾经也以为建模很高深，但其实建模的概念并不难理解。 简单来说，建模就是建立数学模型（modeling），类似于小学应用题中列方程/公式的过程，将客观问题抽象成符号表达。

以计算基础代谢率为例，我们可以将其简化为：

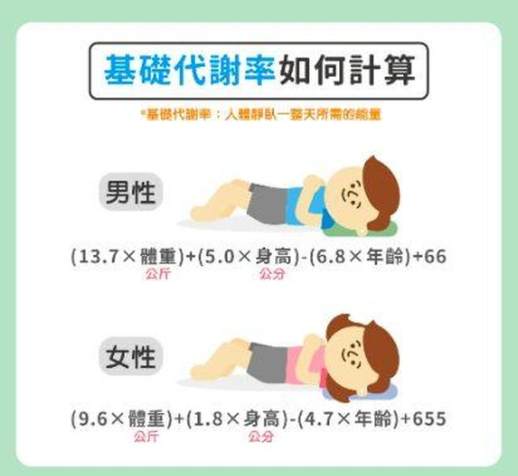
y=ax1+bx2+cx3+d

其中：

y 是要计算的基础代谢率，是因变量（dependent variable）
x1、x2、x3 是自变量（independent variable/argument)，分别代表 体重、身高、年龄
a、b、c 是系数（parameter）, 例如a=9.6说明体重每增加一公斤，基础代谢率就会上升9.6
d 是常数项

在我研究生阶段的统计建模课程中， 我们小组的期末项目应用了课堂上学到的因子分析、聚类分析、决策树模型和逻辑回归模型来预测休克概率。

我记得当时使用的因变量包括血压、血糖等医学指标， 我们对数据进行了分析，并完成了精彩的展示， 最终获得了教授的邮件表扬。

前面我们介绍了建模、参数、因变量、自变量等基本概念， 那么，如何判断一个模型的优劣呢？

本文的技术顾问小斐认为：" 理解问题，选择合适的方法至关重要。 在推荐系统等特定场景下，模型的优劣主要取决于算法， 追求的是最优解和计算效率。 数据也至关重要。 充足的数据是构建优秀模型的前提。 数据决定模型的上限，算法决定模型的下限。"

我认为，除了数据，想象力和敏感度对建模也至关重要。 例如，在进行假设时，我们可以思考基础代谢率是否与其他变量有关：头发长短、手指长度、眼睛大小等等（开个玩笑）。 模型需要不断迭代更新，才能更好地拟合已有数据（训练数据）并进行预测。

为什么数据建模师会自嘲为"调参侠"呢？

这是因为模型需要不断迭代，通过调整模型参数来提高模型对数据的拟合程度。

通过上述例子，我们可以总结出模型的作用：

• 抽象简化： 现实世界中的一些过程比较复杂，难以理解或预测。我们可以尝试将其简化，抽象成数学模型，例如计算基础代谢率。
• 描述/预测：抽象成模型后，我们可以利用模型进行预测，或对已有现象给出合理的解释。模型可以帮助我们理解一个系统，研究不同组成部分的影响，并对行为做出预测。

优秀的模型不一定复杂，根据奥卡姆剃刀原理，在解释度相同的情况下，越简单的模型越优。

只有数学模型吗？ 老板让我做的那些包含奇怪英文缩写的模型是什么？

不可否认，"模型"一词有被滥用的趋势。 并非所有由几个英文单词组成的缩写都能被称为模型。 例如， Sxxx Bxxx 不能被称为 SB 模型， SB 最多只能算作缩写。

在社会科学领域，诸如商业分析、认知研究和思维模式等，都广泛存在着“模型”的概念。简而言之，建模的本质是抽象化。它试图从你关注的对象中提炼出关键特征，并以此构建一个简化的、想象中的事物，用以解释或预测真实世界的现象。这个被构建出来的“事物”，就是我们所说的“模型”。

以行业模型分析为例，我们可以将“框架”理解为多个模型的组合。

题图制作：偶尔动脑公众号

模型的使用不应僵化。如果我们被工具束缚了思维，就会像“手里拿着锤子，看什么都像是钉子”一样，陷入误区。问题的解决应该灵活运用模型和方法。比如，如果可以直接获取到一家公司的研发投入数据，我们就没有必要再费力地使用各种财务模型去推算了。

我认为模型/框架的最大价值在于帮助我们系统、全面地收集信息，并对行业的不同属性进行刻画。这仅仅是完成了整个分析过程的60%。真正考验功力的是如何将这些信息点连接起来，分析它们之间的关系，并提炼出具有共性的结论。

题图制作：偶尔动脑公众号

最近玩了一场德州扑克，让我深刻体会到模型和现实之间的联系。德州扑克的输赢可以简化为以下函数：

f (手中的牌、已经翻的牌、还没翻的牌、对手的牌性、对手的牌、bluffing吹嘘的能力，别人对你吹嘘的信任度、座位位置…..)

每一局的影响因素都在变化，这也正是德州扑克的魅力所在。它就像现实世界一样复杂多变，需要我们灵活运用各种策略和技巧。

免责声明：虽然我研究生学习统计学，但我并非该领域的专家，且多年未接触相关内容，文中观点仅供参考。

本文由@iris 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议