函数收敛

函数是数学的基础概念之一，围绕函数建立了许多重要的数学理论，其中调和函数便是常见且重要的函数类型。它们广泛应用于数学和物理各领域，不仅是重要的研究对象，也是强大的数学工具。今天，我们将浅谈调和函数，以窥探数学的奥妙。

调和函数的历史悠久，可追溯至 19 世纪，当时它们已是重要的数学概念，得到广泛应用。什么是调和函数？需要定义拉普拉斯算子：

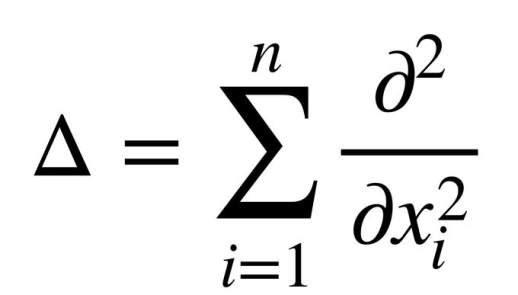
拉普拉斯算子的作用是对不同的自变量求二阶偏导数，然后相加得到一个关于偏导数的函数。调和函数是指经过拉普拉斯算子作用后等于零的函数，即满足以下条件的函数：

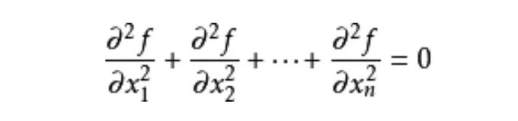
需要注意的是，在定义调和函数之前，要求函数在 R^n 中的某个区域内存在二阶偏导数，且通常要求 n 大于等于 2。

为何调和函数值得研究？简而言之，其特性极其优越，用途广泛。

调和函数的第一个惊人特性是解析性，即在定义域内每一点可进行无穷次泰勒展开。这意味着调和函数是光滑且可无限次微分的。这一特性为何重要？由于在定义调和函数时仅要求其存在二阶偏导数，如此定义仅用最小的要求就能保证函数的光滑性。

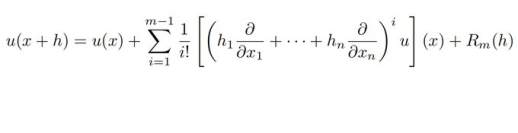
解析性并非调和函数的本质特性。调和函数最核心的性质是满足平均值原理。为了进一步理解调和函数的特性，我们通常会在有界区域内考虑这些问题，并要求函数具有连续或可导的边值。那么，什么是平均值原理呢？简单来说，即函数 u 在一点 x 的值等于函数在以 x 为中心的球区域中体积积分或面积积分的平均值（简单的积分计算表明，这两种积分平均值是等价的）：

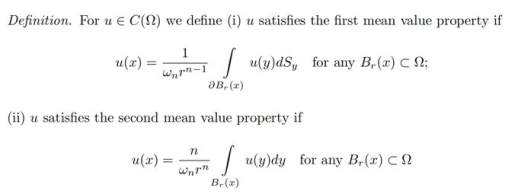
为何平均值原理是调和函数最本质的特征呢？因为调和函数几乎所有重要的特性都可以从平均值原理推导出来，例如上文提到的解析性。更重要的是，平均值性质完全刻画了调和函数，即：

调和函数的另一个重要特性是极值原理：

如果调和函数不是常数，则它在内部不能取到极大值或极小值。

根据极值原理，我们可以立刻得知调和函数完全由其边值唯一决定：

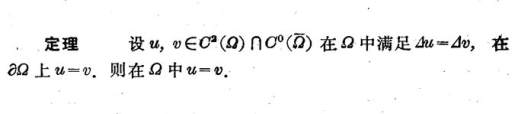
从更高的角度来看调和函数，即把△u=0 的定义看作一个偏微分方程（准确来说是拉普拉斯方程），那么调和函数就是该方程的解，而极值原理告诉我们，在给定边值的情况下，解是唯一的。实际上，如果区域足够特殊（通常是球），我们可以通过边值条件直接求得该解，这又涉及到泊松积分，而泊松积分又与格林函数有关。

格林函数起源于物理中的场论，具体定义在此不详述。但它的作用是用来表示具有边值的这种方程的解。实际上，利用格林函数和拉普拉斯方程的基本解，我们可以得到调和函数的格林表示：

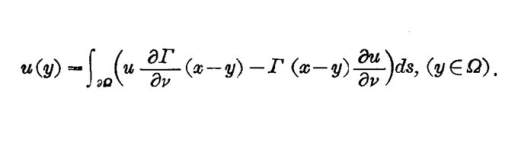
由于被积函数是光滑的，从格林表示中，我们再次获得了调和函数的光滑性。当区域是一个球时，由于区域特殊，我们可以利用几何中的反演方法得到相应格林函数的表达式，从而通过边值求解调和函数成为可能，这就是带边值调和函数的泊松积分表达式：

调和函数还有一个非常重要的性质，即调和函数序列良好的收敛性。在学习数学分析时，级数和函数序列的收敛性是我们非常关注的概念，因为良好的收敛性可以保证极限函数也具有某些好的性质。而从前面提到的平均值原理可以发现，调和函数序列恰好拥有某些良好的收敛性：

一致收敛的调和函数序列的极限函数也是调和的。

进一步，还可以证明：

上述讨论揭示了调和函数诸多优越性质，使其成为偏微分方程、数学物理方法等众多数学分支的关键工具。更令人着迷的是，“调和”的概念已超越实数空间函数的范畴，延伸至微分流形，为研究流形上的调和函数提供了新的视角。“调和”还渗透到更抽象的微分形式领域，与著名的“霍奇理论”建立起深刻联系。 毋庸置疑，调和函数及其推广的应用远不止于此，但其在数学中的重要地位已不言而喻。