奇变偶不变什么意思

三角函数诱导公式用法：
针对形如kπ/2±α（±α加上π/2的k倍）的角，将三角函数值化简为α的三角函数值。
奇变偶不变：
奇变：当kπ/2是π/2的奇数倍时，化简后正弦转换为余弦，余弦转换为正弦。
偶不变：当kπ/2是π/2的偶数倍时，化简后正弦仍然是正弦，余弦仍然是余弦，正切仍然是正切。
符号取象限：
将α视为锐角时，kπ/2±α的三角函数值的正负号要添加到化简后的值上。
依据“一全正、二正弦、三正切、四余弦”，判断三角函数值在四个象限内的正负号。
十字口诀：
记住“奇变偶不变，符号看象限”的口诀，即可推导出所有诱导公式。
具体应用：
对于没有列出的公式形态，如：
-π+α：可以先加上2π变为π+α，再运用诱导公式。
-π/2+α：由于-π/2是π/2的奇数倍，故化简后正弦转换为余弦，且α所在象限为第四象限（正弦为负值），因此化简后带负号。

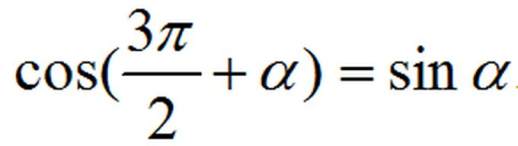
将3π/2视为π/2的奇数倍，根据"奇变偶不变"原则，余弦函数将变换为正弦函数。 将α视为锐角，则3π/2+α位于第四象限。由于第四象限余弦值为正，因此化简后sinα前的符号为正号。