数学家的眼光

作者 | 重庆 辛酉丑
二十多年前,我便知晓张景中教授以消点法解决机器证明平面几何问题,后来又研习了他主编的《好玩的数学》丛书。我们学校使用的湘教版教材也是他主编的,却从未谋面。恰逢重庆师范大学同学告知,才得以参加他此番讲座。
会场座无虚席。大会于 8 点 50 分拉开序幕,六位来自不同地区学校的专家先后发言。间中穿插合影环节。直至 11 点后,才迎来张教授的报告。张教授主要阐述了他的教育数学思想。他提出四个“容易”:熟悉了容易、简单了容易、看清了容易、想通了容易。
张教授的报告不同于教育专家,语言朴实,没有华丽辞藻,白描风格。若由教育专家讲授此话题,或阐述什么是教育数学、其历史渊源、基本原则、研究热点、课堂实践,或如怨妇般抨击应试教育弊端、谴责教师机械刷题、狂吹只有教育数学才真正抓住了数学本质。教育专家报告常引人愤发、催眠、低头玩手机、假装上厕所外出呼吸新鲜空气。

张教授是数学院士,几句话开场,直奔主题。他认为,教育数学应从几何、代数、三角;解析几何、向量;微积分三大方向入手。张教授并非中学校教师,也不任教博士生,直接讲述如何将微积分改造为教育数学。他认为,以极限定义微积分导数、积分等概念,教师难以讲授,学生难以理解。他旨在使微积分熟悉、简单、直观、易懂。
他以瞬时速度和平均速度为例,谈及他花了 50 年才意识到二者之间的关系 —— 平均速度要么大于要么小于瞬时速度。这个朴素结论可用数学语言描述如下:
设函数和都在数集 S 上有定义,若 中的任意两点 ,总存在 中的 ,使得不等式
成立,则称 是 在数集 上的甲函数, 是 在数集 上的乙函数。上述不等式称为估计不等式.

这个看似简单的结论,张教授言称他思考了 50 年,直到 2015 年才想通。花费 50 年精力推导出一个结论,这个效率看似不高,难与教育家相比。且看那些教育家近期提出的教育新发现:有效课堂、高效课堂、卓越课堂、核心素养,比换衣服还快,俨然一场造词比赛。
张教授欲用这个极简事实在教育数学中有所突破。全球数学教材均以极限定义导数,抽象难懂;张教授以这个妇孺皆知的朴素结论定义导数,不用极限,帮助初学者理解导数,对初学者意义非凡,确实发前人之未发。50 年的艰苦历程,让我明白为何我国数学家稀缺,教育家泛滥,甚至不识字的学生家长和匆忙主妇均对教育指手画脚。

张教授不知疲倦地讲解,直至 12 点 20 分结束,其间无人玩手机,也无教师外出吸烟。我强忍尿意,不敢上厕所,唯恐遗漏要点,打断思路。下午我们与张教授一同来到重庆一中,听两位教师讲课。重庆一中 T 教师讲述《正弦函数的新装 ── 与面积的不解之缘》,谈及张教授用面积定义正弦:边长为 ,一个角为 的菱形的面积叫做 的正弦,即 。
重庆八中 S 教师讲述《向量在代数与几何问题中的应用》。随后是与会专家评课环节,最后请张教授点评。80 多岁的老人站立讲授近 50 分钟,过程中多次引起大家鼓掌致谢。我们不仅感受到张教授对数学的热爱和执着,更被他的记忆力和思维力所震撼。
先看 T 教师的课堂:
例 1.在 中,,,,求角平分线 AD 的长。
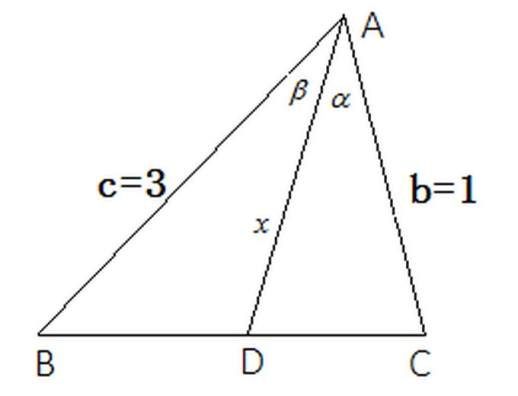
解:,,
由
例 2.直线 ,过点 P(1,1)交直线 和 轴分别于 C,B,求 最大值。
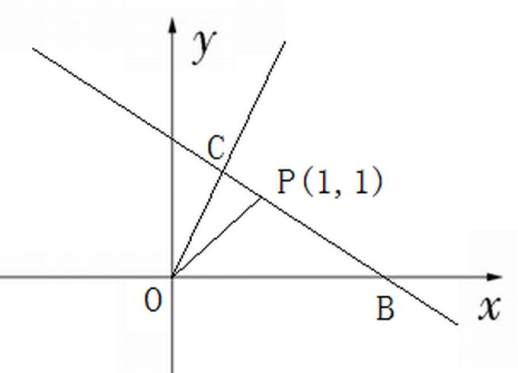
对于例 2,T 教师这样解:令过 得直线为
由题意课求出:
(1)如果
(2)如果
综上,当 时,
T 教师的解法也是中学教师最容易想到的方法,但计算量大,费时费力。
本节课展示此例题,显然适用面积法。T 教师通过复杂运算和大量板书才求出结果。在旁听时我坐在张教授身旁,见他只画了一个图,未作任何记录。点评时,他已察觉了两个例题之间的联系,在场教师无不惊叹于他的洞察力和思维能力。他的解法如下:
由例 1 解答,可以得到一般性结论:.
即,多么优美的等式!她就是传说的张角定理。
对于例 2:用上面结论可得
则
又
同理:
要求 最大值,只需求 的最大值,显然,当 即可.
这两个例题,一个平面几何问题,一个解析几何问题,为了切合课题,大家都知道用面积法,只就题论题,根本没有发现两个例题之间的联系。对于年轻的 T 教师,例题是自己选的,教学也是自己设计的,依然停留在就题论题的层次上。但年过八旬的张教授只画了一个图,未写一个字。不仅从例 1 得到了张角定理,还顺便解答了例 2。无论是思维能力还是数学眼光,都远远超越一般教师。
第二节课是重庆八中 S 教师讲授的《向量在代数与几何问题中的应用》,S 教师用几个代数题的解答来说明向量的应用。如下例题:
例 3.求证:
例 4.已知 ,求证:
以上两个例题并非难题,S 教师快速构造向量解答。评课时张教授的巧妙解答完全颠覆了常人的想象。他的解答如下:
例 3 的解:令 在 上递减,显然上市成立。
例 4 的解:令
显然上市成立。
上述解答正是张教授上午报告中提到的差商,只需研究 和 的导数即可,这也是高观点下的初等数学的一次实践。
对于两位教师课堂上的几个例题,常人看上去确实毫无联系,即便上午听了张教授的报告,依然未能发现例题之间的联系。一个人即使有健康的眼睛,也不一定有良好的数学眼光

