质因数分解器 怎样把一个数分解因数

近日，科学界迎来了一项引人瞩目的突破：中国科学技术大学的潘建伟团队与中科院上海微系统所、国家并行计算机工程技术研究中心合作，成功研制出一款名为“九章”的量子计算原型机。该机能够在短短200秒内完成高斯玻色采样，而利用现今最强大的超级计算机——太湖之光，执行同样的计算却需耗时长达20亿年。如此巨大的差距，引发了人们对量子计算技术的广泛关注。

九章

在众多好奇的声音中，有小朋友提出了疑问：“九章计算机真的这么快吗？玻色采样问题是什么？它能否破解我们的银行密码呢？”针对这些问题，本文将深入探讨九章的工作原理及其潜在应用。

要理解九章的原理，首先需要掌握一些数学概念。本文将围绕这些概念展开讨论，虽然过程可能显得较为复杂，但最终将揭示九章的强大之处。欢迎大家留言讨论，但请注意保持理性，避免无谓争论。

高尔顿钉板

为了更好地理解九章的原理，我们可以从高尔顿钉板的实验说起。街头常见的一种抽奖游戏就是将小球扔进布满钉子的盒子，经过钉子的多次碰撞后，小球最终会掉入某个槽中，根据槽的位置来决定获奖的情况。

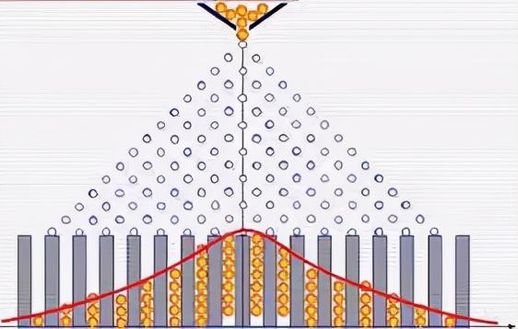
钉板游戏

这种装置是由19世纪的英国学者高尔顿所发明的。在这个过程中，小球落入各个槽中的概率与其碰撞的方式密切相关。以一个有4行钉子的钉板为例，如果小球要掉入最左或最右槽，必须全程向左或向右运动，这样的路径只有1种。若小球要到达A槽，则可以有两种路径：从左上到达或从右上到达A。小球到达A槽的方法数等于左上和右上路径数的总和，A=1+1=2。

通过这种规律，我们可以列出小球到达任意位置的方法数，从而形成一个杨辉三角。每次碰撞后，小球向左或向右的概率均为1/2，因此落入某个槽的方法数越多，该槽的概率也就越高。若槽的数量不断增加，计算每个槽的概率将变得非常复杂。这时，我们可以考虑使用采样法，通过多次实验来获取各个槽的小球落入频率，从而推导出概率。

这个物理实验通过实践得出概率，再利用此概率反向计算复杂的数学问题，这种方法在历史上得到了广泛应用，例如著名的蒲丰投针实验。

行列式

回到量子计算机“九章”，它所解决的问题与线性代数中的行列式密切相关。行列式是一个从矩阵中派生出的重要概念。例如，对于一个2x2矩阵，我们可以通过简单的乘法和减法来求得它的行列式。

行列式在数学和物理中的应用极为广泛，例如计算两个平面向量构成的平行四边形的面积等。随着矩阵维度的增加，行列式的计算变得愈加复杂。但值得注意的是，行列式有很多优良性质，使其计算相对高效。

积和式

与行列式相对的是积和式，它的计算复杂度要高得多。尽管它与行列式有着类似的形式，但计算积和式的难度随着维度的提升而呈指数级增长。在这种情况下，传统的计算方法显得无能为力。

面对这种困境，历史上常常通过物理实验来辅助计算。例如，伽利略利用滚动铁片的方法获得了摆线的面积，这也为我们解决积和式的问题提供了启示。

在量子物理中，玻色采样问题则成为了计算积和式的一个有效途径。光子作为玻色子，能够在相同状态下存在多个粒子，这一特性使得我们能够通过整体波函数来描述粒子的分布概率。麻省理工学院的教授阿伦森和他的博士生阿尔希波夫证明，玻色采样问题的粒子分布概率与积和式的模方成正比。

九章的实验装置实际上就如同一个光子的高尔顿钉板，通过精确的光子干涉与探测，实现了对玻色采样的快速计算。这一过程的实现，意味着我们能够在量子层面迅速获取概率，从而反向推导出积和式。

尽管九章展示了惊人的计算能力，值得注意的是它依然是一个原型机，并非通用计算机。它的优势在于特定问题上的表现，而对于一些复杂的任务，经典计算机依旧展现出强大的通用性和灵活性。尽管量子计算的时代正在到来，但距离广泛应用还有很长的路要走。

在当前阶段，我们的银行密码依然安全，量子计算机尚未具备破解这一复杂问题的能力。未来，随着量子技术的不断发展，我们或许能够迎来真正的量子计算革命，但在许多日常应用场景中，经典计算机仍然占据重要地位。量子霸权的到来，依旧任重道远。