线性相关系数公式 统计学线性相关系数
如何比较两个相关系数的差异?
在实际研究中,我们经常需要比较同一个变量与其他多个变量之间的线性相关性强弱。例如,我们想知道变量A与B、C之间的相关性强弱,即A与B更相关还是与C更相关?
我们需要分别计算A与B、A与C之间的简单线性相关系数,并进行假设检验。只有当两个相关系数均具有统计学意义(即p值均小于0.05)时,我们才有必要进一步比较它们的差异。
例如,下图展示了A与B(蓝色线)和A与C(橙色线)之间的线性关系。
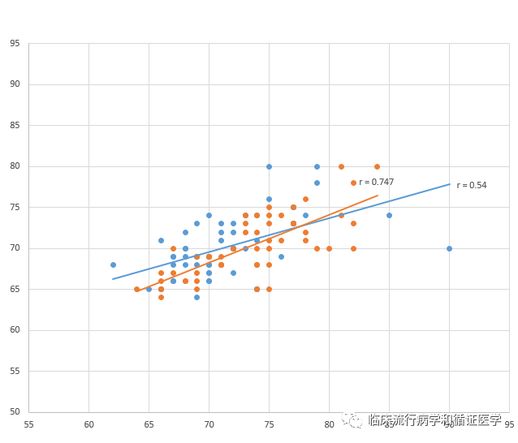
SPSS软件分析结果显示,A与B的相关系数r_AB=0.54(p<0.001),A与C的相关系数r_AC=0.747(p<0.001)。仅仅根据相关系数的大小判断,r_AC>r_AB,似乎A与C之间的相关性更强。这种比较方式并不严谨。
为了更准确地比较两个相关系数的差异,我们需要借助统计学方法。
方法一:比较置信区间
我们可以分别计算两个相关系数的置信区间,并观察它们是否存在重叠。如果两个置信区间没有重叠,则说明两个相关系数之间存在显著差异。反之,则说明差异不显著。
在SPSS中,我们可以通过自助抽样(Bootstrap)方法轻松获得相关系数的置信区间。

结果显示,r_AB的置信区间为0.353至0.747,r_AC的置信区间为0.618~0.857。由于两个置信区间存在重叠,因此我们认为A与B、A与C之间的相关性差异无统计学意义。
方法二:假设检验
另一种方法是利用假设检验直接比较两个相关系数的差异。该方法需要使用相关系数r和样本量n计算u值:

u值服从标准正态分布。如果u>1.96或u<-1.96,则p<0.05,说明两个相关系数之间存在显著差异;如果-1.96<u<1.96,则p>0.05,说明差异不显著。
在本例中,u=-1.828,位于-1.96和1.96之间,因此p>0.05,说明A与B、A与C之间的相关性差异无统计学意义。需要注意的是,如果相关系数为负数,我们需要取其绝对值进行比较。
仅仅比较相关系数的大小并不能得出可靠的结论,我们需要结合置信区间或假设检验等统计学方法来判断两个相关系数之间是否存在显著差异。
---
作者:杨老师 (中国统计邀认证作者)
本文为头条号作者原创。未经允许,不得转载。
运行人员:中国统计网小编(微信号:itongjilove)
中国统计网,是国内最早的大数据学习网站,公众号:中国统计网
http://www.itongji.cn

