什么是方程的增根

分式方程中的“隐形陷阱”：增根

同学们好，我是刘小龙老师！今天我们来揭秘分式方程中容易被忽视的“隐形陷阱”——增根。

很多同学在解分式方程时，以为求出x的值就大功告成了，却忽略了验证。实际上，有些看似正确的解，代入原方程却会让分母变成0，导致无法计算，这就是我们所说的“增根”。

为什么会出现增根呢？

我们都知道，6除以0是不存在的，因为6个苹果无法分给0个人。同样，2不等于3，但如果两边同时乘以0，就变成了0等于0，看似成立，但实际上毫无意义。

解分式方程时，为了消去分母，我们会将方程两边同时乘以分母的最小公倍数。这个操作本身没有问题，但如果解出的x值恰好让原方程的分母为0，就会导致出现“增根”。

例如，在一个分式方程中，我们解得x=4。但将x=4代入原方程后发现，分母变成了0，导致整个式子无法计算。这就好像我们把2和3同时乘以了0，得到了看似相等的0=0，但实际上2依然不等于3。

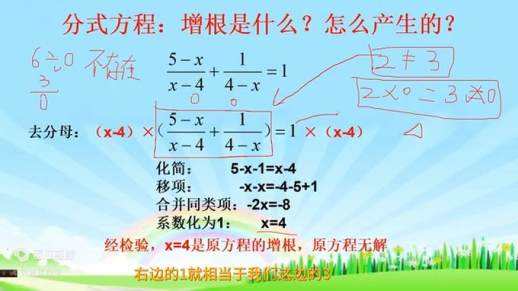
x=4就是这个方程的“增根”，它并不是原方程真正的解。在解题过程中，我们必须进行检验，排除增根，才能得到正确的答案。

检验的方法很简单，就是将解出的x值代入原方程，如果等式成立，则说明该解是原方程的解；如果等式不成立，则说明该解是增根，需要舍去。

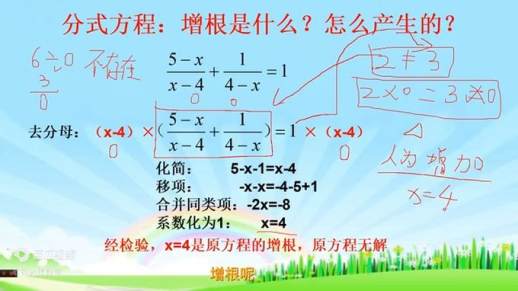
记住，解分式方程的最后一步一定是“验根”！无论是考试还是实际应用中，这都是至关重要的一步，可以帮助我们避免因为“增根”而得出错误的结论。

希望同学们通过今天的学习，能够更好地理解和掌握分式方程的解法，避免掉入“增根”的陷阱中！下期再见！